分治算法之最大子数组问题
1. 前言
本节内容是分治算法系列之一:最大子数组问题,主要讲解了什么是最大子数组问题,如何利用分治算法解决最大子数组问题,给出了最大子数组的实现伪代码并进行分析,并用 java 语言进行了伪代码实现,帮助大家通过最大子数组问题更好地理解分治算法思想的应用。
2. 什么是最大子数组问题?
最大子数组(Max Subarray)问题,是计算机科学与技术领域中一种常见的算法问题,主要可以利用分治思想进行快速实现。
最大子数组问题描述如下:假如我们有一个数组,数组中的元素有正数和负数,如何在数组中找到一段连续的子数组,使得子数组各个元素之和最大。
最大子数组问题在生活中有很多实际情况可以与其对应,比如说我们观察某一股票在一段时间内的走势,请问如何找出在哪一天买入,哪一天卖出可以赚到最大差价(这里假设你已经知道股票的价格走势)?为了实现最大化的股票收益,我们需要考虑的是买进和卖出时候的价格变化幅度,因此从该股票的每日变化幅度来考虑这个问题更加合适。所以,我们可以将这个问题稍作变形:将股票价格走势对应为每日股票价格涨跌,涨记为正值,跌记为负值,然后一段时间就对应一个正负数数组,并试图找到该数组的最大子数组,就可以获得最大收益。
接下来,就让我们看看如何利用分治算法求解最大子数组问题吧。
3. 分治法求解最大子数组问题
在最大子数组问题之后,我们一起来看一下如何利用分治思想求解最大子数组问题。这里我们假设待初始的数组为 [12, -3, -16, 20, -19, -3, 18, 20, -7, 12, -9, 7, -10],记为数组 A,并用 A [low,high] 表示这个数组,其中 low,high 是这个数组的最小最大下标, low = 0,high = A.length -1 , 然后我们需要找到该数组的其中某一个最大子数组。
Tips: 这里我们需要注意,同一数组的最大子数组可能有多个,所以我们在这里求解的时候只说求解某一个最大子数组。
3.1 分治算法求解思路
在这里,我们用分治算法求解最大子数组问题,主要思路如下:
- 步骤 1:
找到数组 A 的中间元素,其下标记为 mid,根据分治策略,将数组 A [low,high] 根据中间元素划分为 A [low,mid], A [mid+1,high] 两个部分; 2. 步骤 2:
假设数组 A 的最大子数组为 A [i, j],那么 A [i, j] 只有以下三种可能:
a: 最大子数组 A [i, j] 完全位于 A [low, mid] 中,此时有 low <= i <= j <= mid;
b: 最大子数组 A [i, j] 完全位于 A [mid+1, high] 中,此时有 mid+1 <= i <= j <= high;
c: 最大子数组 A [i, j] 跨域了中间元素,则 low <= i <= mid <= j <= high。
分别计算上述三种对应的最大子数组的结果;
Tips: 在这里,情况 a 和情况 b 这两种情况所得的子问题和之前求解数组 A 的最大子数组的问题形式完全一样,这里是分治思想的主要体现,将大的问题拆分成了两个相同形式的小问题;情况 c 这时候可以直接求解,在 3.2 节中会具体介绍其求解过程。
- 步骤 3
对步骤 2 三种情况的求解结果进行比较,其中最大子数组的结果为最大值的情况就是我们的所求结果。
3.2 求解思路详解
首先,我们将 3.1 节中的求解思路用下图表示:
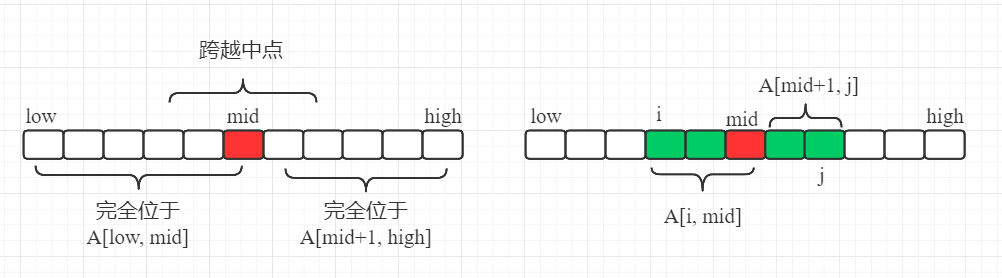
如图,我们可以更清楚地明白求解一个数组的最大子数组问题就是对 3.1 节中的步骤 2 中的三种情况的分别求解, 步骤 2 中的情况 a 和情况 b 可以通过递归求解得出结果,所以我们现在先看一下情况 c 的具体求解过程。情况 c 的求解很容易在线性时间内就可以得出结果,他并不是原问题的一个规模更小的实例,因为情况 c 中加入了一个限制(求出的子数组必须跨越下标为 mid 的中间节点)。如上图的右边图形所示,情况 c 的求解结果都会有两个子数组 A [i,mid] 和 A [mid+1,j] 组成,其中 low <= i <= mid <= j <=high。因此,我们只需要找出形如 A [i,mid] 和 A [mid+1,j] 的最大子数组,然后将其合并即可。
我们用下面的伪代码 FindMaxCrossSubarray 描述 3.1 节中 步骤 2 中的情况 c 具体实现过程:
FindMaxCrossSubarray(A, low, mid ,high):
leftSum = minInteger; //设置左边的最大连续和初始值为最小整数值
sum =0;
maxLeft = mid; //记录左边最大子数组的下标位置,初始化为mid
for (i=mid; i>=low; i--){
sum = sum + A[i];
if (sum > leftSum){
leftSum = sum;
maxtLeft = i;
}
}
rightSum = minInteger; //设置右边的最大连续和初始值为最小整数值
sum = 0;
maxtRight = mid + 1; //记录右边最大子数组的下标位置,初始化为mid+1
for (j=mid+1; j<=low; j++){
sum = sum + A[j];
if (sum > rightSum){
rightSum = sum;
maxtRight = j;//记录左边最大子数组的下标位置
}
}
//返回结果是一个三元组数据,分别是最大子数组的开始下标,结束下标,求和的值
return (maxLeft,maxRight,leftSum+rightSum);
上述伪代码的描述中的第 2 至第 11 行,是求解左半部分 A [low,mid] 的最大子数组的过程,因为必须包含下标为 mid 的元素,所以从下标为 mid 的中间节点开始逐步递减到下标为 low 的元素,对应伪代码中的第 5 至第 11 行的 for 循环结构,循环的过程中会记录下左边部分的最大子数组的具体值及左半部分的下标位置。同理,上述伪代码的第 12 至第 21 行对应的是求解右半部分 A [mid+1,high] 的最大子数组的过程。最后,伪代码中的第 23 行综合左右两边求解结果,返回必须跨越下标为 mid 的中间元素时,对应的原数组 A 的最大子数组结果。
当我们可以清楚地知道步骤 2 中的情况 c 的求解过程时,我们就可以综合知道对于数组 A 求解最大子数组的整体过程,用伪代码 FindMaxSubarray 描述如下:
FindMaxSubarray(A,low,high):
if (high == low){
return new Result(low,high,A[low]); //基础情况,只有一个元素时候的处理情况
}else {
//对应2.1节中步骤1,找到中间元素
int mid = (low + high)/2;
//对应2.1节中步骤2,分别对应a,b,c三种情况求解最大子数组结果
(leftLow,leftHigh,leftSum) = FindMaxSubarray(A,low,mid);
(rightLow,rightHigh,rightSum) = FindMaxSubarray(A,mid+1,high);
(crossLow,crossHigh,crossSum) = FindMaxCrossSubarray(A,low,mid,high);
//对应2.1节中步骤3,比较得出最后结果
if(leftSum >= righSum && leftSum >= crossSum){
return (leftLow,leftHigh,leftSum);
}else if (rightSum >= leftSum && rightSum >= crossSum){
return (rightLow,rightHigh,rightSum);
}else {
return (crossLow,crossHigh,crossSum);
}
}
上述求解数组 A 的最大子数组的整体过程伪代码,主要就是由我们在 2.1 节中描述的三大步骤而来。代码第 2 至第 4 行,主要表明了最基础的情况的处理方式。代码第 4 至第 18 行对应着具体的实现方式,第 8 行和第 9 行分别是对子问题的递归求解,第 10 行调用 FindMaxCrossSubarray 过程,求解跨越中间节点的最大子数组求解方式,最后第 12 至 18 行对比三种情况的结果得出最终结果。
4.JAVA 代码实现
在说明求解最大子数组的整个过程之后,接下来,我们看看如何用 java 代码实现最大子数组问题的求解。
package divide_and_conquer;
public class MaxSubarray {
//内部类,用来存储最大子数组的返回结果,
private static class Result {
int low;
int high;
int sum;
public Result(int low, int high, int sum) {
this.low = low;
this.high = high;
this.sum = sum;
}
@Override
public String toString() {
return "Result{" +
"low=" + low +
", high=" + high +
", sum=" + sum +
'}';
}
}
private static Result FindMaxCrossSubarray(int[]A,int low, int mid, int high){
//寻找左边的连续最大值及记录位置
int leftSum = Integer.MIN_VALUE;
int sum = 0;
int maxLeft = mid;
for (int i=mid; i>=low; i--){
sum = sum + A[i];
if(sum > leftSum){
leftSum = sum;
maxLeft = i;
}
}
//寻找右边的连续最大值及记录位置
int rightSum = Integer.MIN_VALUE;
int maxRight = mid+1;
sum = 0;
for ( int j=mid+1; j<=high;j++){
sum = sum + A[j];
if(sum > rightSum){
rightSum = sum;
maxRight = j;
}
}
//返回跨越中间值的最大子数组结果
return new Result(maxLeft,maxRight,leftSum + rightSum);
}
public static Result FindMaxSubarray(int[] A, int low, int high){
//数组只有一个元素时的处理情况
if (high == low){
return new Result(low,high,A[low]);
}else {
//对应思路中步骤1,找到中间元素
int mid = (low + high)/2;
//对应思路中步骤2,分别对应a,b,c三种情况求解最大子数组结果
Result leftResult = FindMaxSubarray(A,low,mid);
Result rightResult = FindMaxSubarray(A,mid+1,high);
Result crossResult = FindMaxCrossSubarray(A,low,mid,high);
//对应步骤3,比较
if(leftResult.sum >= rightResult.sum && leftResult.sum >= crossResult.sum){
return leftResult;
}else if (rightResult.sum >= leftResult.sum && rightResult.sum >= crossResult.sum){
return rightResult;
}else {
return crossResult;
}
}
}
public static void main(String[] args){
int[] A = {12, -3, -16, 20, -19, -3, 18, 20, -7, 12, -9, 7, -10};
System.out.println(FindMaxSubarray(A,0,A.length-1).toString());
}
}
运行结果如下:
Result{low=6, high=9, sum=43}
运行结果中的 low 表示最大子数组在数组 A 中的开始下标,high 表示最大子数组在数组 A 中的终止下标,sum 表示最大子数组的求和值,对应到我们的实例数组 A 中,对应的最大最大子数组为 [18,20,-7,12]。
代码中第 5 行至 25 行的 Result 内部类,主要是用来存储最大子数组的返回结果,定义了子数组的开始下标,结束下标,求和值。代码的第 27 至 55 行是最大子数组跨越中间节点时候的最大子数组求解过程。代码的第 58 至 78 行是整个最大子数组的求解过程。代码的第 81 行和 82 行是求解最大子数组过程的一个示例,输出最大子数组的求解结果。
5. 小结
本节主要学习了利用分治思想求解最大子数组问题,学习本节课程需要熟悉分治算法的算法流程,知道分治算法在解决最大子数组时的实现思路,可以自己用代码实现最大子数组问题的求解。在学习完本节课程之后,我们通过最大子数组这一实例介绍了分治算法的实际应用,帮助大家可以更好地理解分治算法。