Markdown 数学公式
1. 前言
在专业的学术论文中,数学公式往往是不可或缺的。在 Word 中,想表达出一个复杂的公式非常繁琐,幸运的是 Markdown 其语法中,支持使用 LaTeX 语法实现在文档中插入数学公式。
环境说明:
考虑到 Markdown 工具之间的不兼容,有的内容直接从页面复制粘贴到本地不会正常显示,大家学习时自己动手写是肯定没问题的。本节所有实例代码及演示效果均使用 Typora 工具完成。
LaTex 是 Markdown 扩展功能,需要在 Typora 中开启 LaTex 支持,具体方式为:「设置」-> 「Markdown」->「Markdown 扩展语法」-> 勾选「内联公式」,如下图:
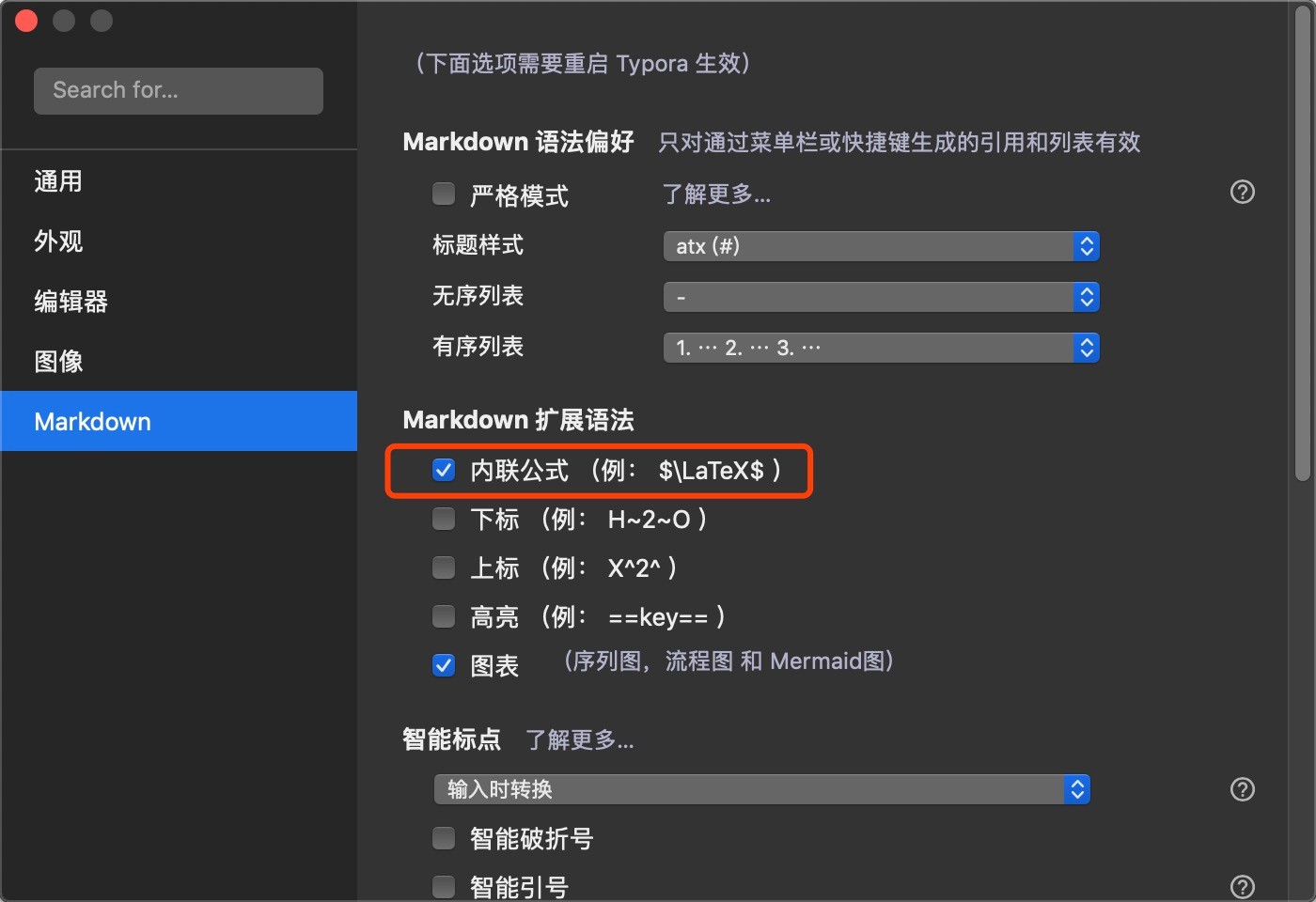
2. 语法详解
2.1 公式的声明
Markdown 中的数学公式也分为「行中公式」和「独立公式」两种。
2.1.1 行中公式
行中公式使用两个单独的「美元符 $」表示。
实例 1:
$1 + 1 = 2$
其渲染效果如下:
2.1.1 独立公式
独立公式的写法是将公式两边用两个连续的「美元符 $$」包裹,换行通过在行尾添加 \\ 实现。
实例 2:
$$
x + y = 10 \\
x - y = 6 \\
2x = 16 \\
x = 8 \\
y = 2
$$
其渲染效果如下:
2.2 运算符
2.2.1 四则运算符
四则运算符是理工运算中的基础,主要包含加减乘除和绝对值运算。
实例 3:
四则运算符号汇总。
加法符号:$x+y=z$
减法符号:$x-y=z$
加减符号:$x \pm y=z$
减加符号:$x \mp y=z$
叉乘符号:$x \times y=z$
点乘符号:$x \cdot y=z$
星乘符号:$x \ast y=z$
除法符号:$x \div y=z$
斜除符号:$x/y=z$
分式1:$\frac{x+y}{y+z}$
分式2:${x+y} \over {y+z}$
绝对值:$|x+y|$
其渲染效果如下:

2.2.2 逻辑运算符
实例 4:
逻辑运算符号汇总。
等于符号:$x+y=z$
大于符号:$x+y>z$
小于符号:$x+y<z$
大于等于符号:$x+y \geq z$
小于等于符号:$x+y \leq z$
不等于符号:$x+y \neq z$
不大于等于符号:$x+y \ngeq z$
不大于等于符号:$x+y \not\geq z$
不小于等于符号:$x+y \nleq z$
不小于等于符号:$x+y \not\leq z$
约等于符号:$x+y \approx z$
恒定等于符号:$x+y \equiv z$
其渲染效果如下:

2.2.3 高等运算符
实例 5:
高等运算符号汇总。
平均数符号:$\overline{xyz}$
开二次方符号:$\sqrt x$
开方符号:$\sqrt[3]{x+y}$
对数符号:$\log(x)$
极限符号:$\lim^{x \to \infty}\_{y \to 0}{\frac{x}{y}}$
极限符号:$\displaystyle \lim^{x \to \infty}\_{y \to 0}{\frac{x}{y}}$
求和符号:$\sum^{x \to \infty}\_{y \to 0}{\frac{x}{y}}$
求和符号:$\displaystyle \sum^{x \to \infty}\_{y \to 0}{\frac{x}{y}}$
积分符号:$\int^{\infty}\_{0}{xdx}$
积分符号:$\displaystyle \int^{\infty}\_{0}{xdx}$
微分符号:`\partial`,如:$\frac{\partial x}{\partial y}$
矩阵符号:$\left[ \begin{matrix} &1 &2 &\cdots &4 &5 &6 &\cdots &8\\ &\vdots &\ddots &\cdots &13 &14 &15 &\cdots &16\end{matrix} \right]$
其渲染效果如下:

2.3 上标、下标
不同于上一节所示上标、下标,在数学公式中有一种更为简单的定义方式。
实例 6:
上标符号:$x^2$
下标符号:$y_1$
组合符号:$a^{x^{2}+y^{2}}$
其渲染效果如下:
2.4 希腊字母
在 Markdown 文档的公式中插入希腊字母的方法是,在美元符号包裹住的中间,直接插入 LaTeX 形式的希腊字母语法即可。
实例 7:
阿尔法:$\Alpha$,$\alpha$
贝塔:$\Beta$,$\beta$
伽玛:$\Gamma$,$\gamma$
德尔塔:$\Delta$,$\delta$
艾普西龙:$\Epsilon$,$\epsilon$
捷塔:$\Zeta$,$\zeta$
依塔:$\Eta$,$\eta$
西塔:$\Theta$,$\theta$
艾欧塔:$\Iota$,$\iota$
喀帕:$\Kappa$,$\kappa$
拉姆达:$\Lambda$,$\lambda$
缪:$\Mu$,$\mu$
拗:$\Nu$,$\nu$
克西:$\Xi$,$\xi$
欧麦克轮:$\Omicron$,$\omicron$
派:$\Pi$,$\pi$
柔:$\Rho$,$\rho$
西格玛:$\Sigma$,$\sigma$
套:$\Tau$,$\tau$
宇普西龙:$\Upsilon$,$\upsilon$
发艾:$\Phi$,$\phi$
器:$\Chi$,$\chi$
普赛:$\Psi$,$\psi$
欧米伽:$\Omega$,$\omega$
其渲染效果如下:

这里需要注意:希腊字母区分大小写,其大小写的定义跟随公式中,声明该希腊字母的语法的首字母大小写。
3. 使用场景及实例
数学公式常出现在算法描述或专业论文之中,是提升文章可读性和专业感的重要手段。
实例 8:
等比数列的通项公式。
$$
a\_n = a\_1q^{n-1}= \frac {a\_1}{q} \cdot q^n(n \in N^\*) \\
其中前 n 项的和公式为:\\
S\_n = \left\{
\begin{aligned}
\frac {a\_1 \cdot (1-q^n)}{1-q} &,q \neq 1 \\
na\_1 &,q=1
\end{aligned}
\right.
$$
其渲染效果如下:

4. 小结
- Markdown 可以扩展对 LaTeX 的支持,使得文本有能力渲染成数学公式;
- Markdown 的同时支持行内公式及独立公式;
- Markdown 的数学公式语法与 LaTeX 定义一致。