动态规划算法实战
本小节会以 leetcode 上的 4 道编程题来进行动态规划算法的实战,以帮助大家更好的理解和掌握动态规划算法。
1. 一维DP
1.1 题目1:买卖股票的最佳时机
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
如果你最多只允许完成一笔交易(即买入和卖出一支股票一次),设计一个算法来计算你所能获取的最大利润。
注意:你不能在买入股票前卖出股票。
示例 1:
输入: [7,1,5,3,6,4]
输出: 5
解释: 在第2天(股票价格=1)的时候买入,在第5天(股票价格=6)的时候卖出,最大利润=6-1=5 。注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
示例 2:
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
这样的典型一维 DP 问题,我们会先思考下如何定义问题的状态,如何能得到递推关系?假设我定义这样一个和股票数据相同大小的列表 F[x],表示以位置 x 结尾时能获得的最大利润,将这个作为问题的状态。容易分析其状态转移方程如下,其中 minVal 等于 nums[0:x-1] 中的最小值:
F[x]=max(F[x−1],nums[x]−minVal) F[x]=max(F[x-1],nums[x]-minVal) F[x]=max(F[x−1],nums[x]−minVal)
示意图如下:
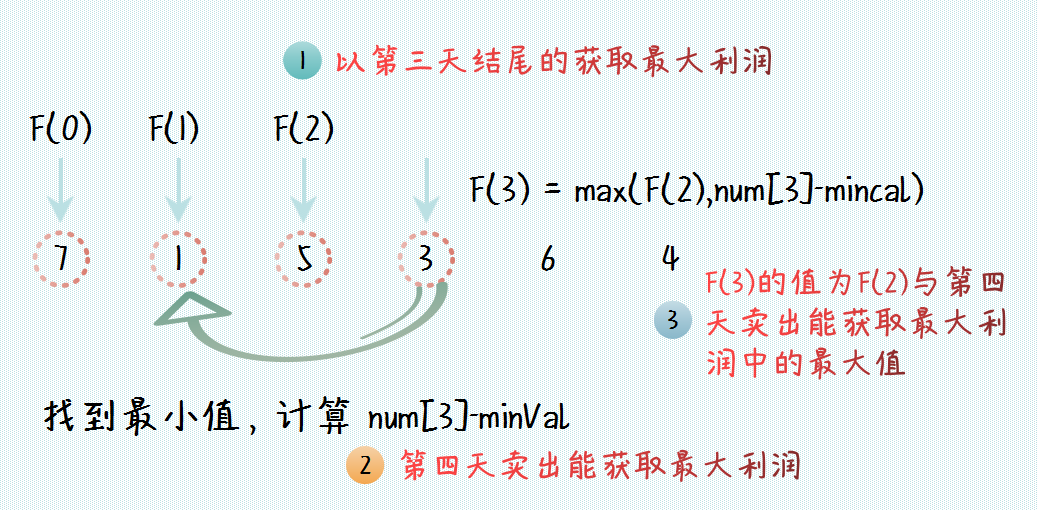
买卖股票状态方程递推示意图
初始的状态条件自然是 F[0] = 0,接下来我们根据上面的 DP 过程完成相应的代码,如下:
class Solution:
def maxProfit(self, prices: List[int]) -> int:
n = len(prices)
if n == 0: return 0
dp = [0] \* n
minVal = prices[0]
for i in range(1, n):
minVal = min(minVal, prices[i])
dp[i] = max(dp[i - 1], prices[i] - minVal)
return dp[-1]
1.2 题目2:打家劫舍
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例 1:
输入: [1,2,3,1]
输出: 4
解释: 偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
示例2:
输入: [2,7,9,3,1]
输出: 12
解释: 偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。
这个同样也是一维 DP 问题,我们这样思考下,定义两个状态数组 F 和 M,其含义分别如下:
- F[x]F[x]F[x]:小偷偷窃到 x 位置的房屋为止,且最后偷窃 x 位置的房屋,此时偷窃的最大金额值
- M[x]M[x]M[x]:小偷偷窃到 x 位置的房屋为止,且最后没有偷窃 x 位置的房屋,此时偷窃的最大金额值
那这样可以得到这样的递推方程:
F[x]=M[x−1]+nums[x]M[x]=max(F[x−1],M[x−1]) \begin{aligned} &F[x] = M[x-1] + nums[x]\ &M[x] = max(F[x-1], M[x-1]) \end{aligned} F[x]=M[x−1]+nums[x]M[x]=max(F[x−1],M[x−1])
最后我们的结果为:
result=max(F[−1],M[−1]) result = max(F[-1], M[-1]) result=max(F[−1],M[−1])
这样可以得到如下的 DP 代码:
class Solution:
def rob(self, nums):
if not nums:
return 0
# 初始条件
F = [0] \* len(nums)
M = [0] \* len(nums)
# 初始条件
F[0] = nums[0]
M[0] = 0
for i in range(1, len(nums)):
# 得到状态转移方程
F[i] = M[i - 1] + nums[i]
M[i] = max(F[i - 1], M[i - 1])
# 返回最后结果
return max(F[-1], M[-1])
2. 二维 DP
2.1 题目1:不同路径
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。问总共有多少条不同的路径?
这题和前面递归中讲解的爬楼梯问题非常相似,我们也可以和之前一样使用递归算法完成解答。但是爬楼梯以及该问题中使用递归存在大量的重复计算,我们要考虑是用 DP 方法来解决该问题。这是一个二维的网格,因此对于 DP 问题而言,我们要考虑二维 DP。定义如下二维 DP 数组 P[i][j]P[i][j]P[i][j] ,表示到(i,j)(i,j)(i,j)位置的不同路径数。
有了这样一个状态的定义,来看相应的递归方程。注意到机器人只能向下或者向右移动一步,因此有:
P[i][j]=P[i−1][j]+P[i][j−1] P[i][j]=P[i-1][j] + P[i][j-1] P[i][j]=P[i−1][j]+P[i][j−1]
初始状态也非常容易,有:
P[i][0]=1(i=0,⋯,m)P[0][j]=1(j=0,⋯,n) \begin{aligned} &P[i][0]=1(i=0,\cdots,m)\ &P[0][j]=1(j=0,\cdots,n) \end{aligned} P[i][0]=1(i=0,⋯,m)P[0][j]=1(j=0,⋯,n)
于是可以立马写出相应的 DP 答案:
class Solution:
def uniquePaths(self, m, n):
if not m or not n:
return 0
P = []
# 保证 P[i][0]=1,P[0][j]=1,即可。其余位置将会递推得到
for i in range(m):
P.append([1] \* n)
# 动态转移方程
for i in range(1, m):
for j in range(1, n):
P[i][j] = P[i-1][j] + P[i][j-1]
return P[-1][-1]
2.2 题目2:最长公共子序列(LCS)
给定两个字符串 text1 和 text2,返回这两个字符串的最长公共子序列的长度。
一个字符串的子序列是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,“ace” 是 “abcde” 的子序列,但 “aec” 不是 “abcde” 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。
若这两个字符串没有公共子序列,则返回 0。
示例1:
输入:text1 = "abcde", text2 = "ace"
输出:3
解释:最长公共子序列是 "ace",它的长度为 3。
示例2:
输入:text1 = "abc", text2 = "abc"
输出:3
解释:最长公共子序列是 "abc",它的长度为 3。
示例3:
输入:text1 = "abc", text2 = "def"
输出:0
解释:两个字符串没有公共子序列,返回 0。
这个也是非常经典的一道面试题,它的解法也是典型的二维动态规划。我们继续按照上面的步骤来定义问题的状态数组以及推导相应的状态转移方程。
我们和前面一样用一个二维的状态矩阵来递推该问题,假设二维状态矩阵如下:
- P[i][j]P[i][j]P[i][j]:表示 text1[0:i] 和 text2[0:j] 的最长公共子序列的长度。
现在来看图说明该二维状态矩阵以及从中推导出状态转移方程:
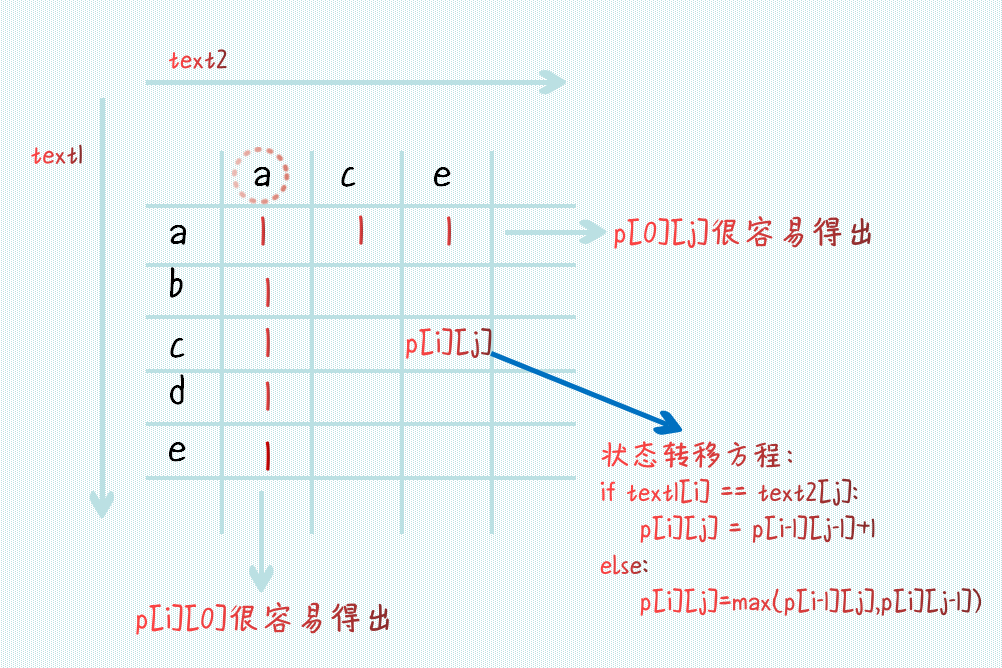
LCS的状态矩阵示意图 容易递推出状态转移方程:
P[i][j]=P[i−1][j−1]+1(text1[i]==text2[j])ormax(P[i−1][j],P[i][j−1])(text1[i]!=text2[j]) \begin{aligned} &P[i][j]=P[i-1][j-1]+1(text1[i]==text2[j]) \ &or \; max(P[i-1][j], P[i][j-1])(text1[i]!=text2[j]) \end{aligned} P[i][j]=P[i−1][j−1]+1(text1[i]==text2[j])ormax(P[i−1][j],P[i][j−1])(text1[i]!=text2[j])
这样我们很容易就能写出相应的 DP 代码,如下:
class Solution:
def longestCommonSubsequence(self, text1: str, text2: str) -> int:
if not text1 or not text2:
return 0
# 初始状态矩阵
P = []
for _ in range(len(text1)):
P.append([0] \* len(text2))
# 编写初始状态,以下两个for循环主要是处理一些边界问题
for j in range(len(text2)):
if j == 0:
P[0][j] = 1 if text2[j] == text1[0] else 0
else:
P[0][j] = max(P[0][j-1], 1 if text2[j] == text1[0] else 0)
for i in range(len(text1)):
if i == 0:
P[i][0] = 1 if text1[i] == text2[0] else 0
else:
P[i][0] = max(P[i-1][0], 1 if text1[i] == text2[0] else 0)
# 核心部分,状态转移方程
for i in range(1, len(text1)):
for j in range(1, len(text2)):
# 上面图片中推到的状态转移方程
if text1[i] == text2[j]:
P[i][j] = P[i-1][j-1] + 1
else:
P[i][j] = max(P[i-1][j], P[i][j-1])
return P[-1][-1]
3. 小结
本小节中我们以 4 道代表性题目给大家展示了如何求解动态规划问题,在 leetcode 上还有许许多多更为复杂和为烧脑的动态规划题目,大家要多多练习,达到熟能生巧的地步。