递归算法介绍
本节将主要介绍基础算法中最为常见和最为简单的算法:递归算法。
1. 递归算法原理详解
递归算法,通常是把一个大型复杂的问题,一次次通过递归调用而层层转化为一个与原问题相似的规模较小的问题来求解,基本思想是将大问题一步步化为小问题,递归算法只需少量的程序就可表达对大问题的计算过程所需要的多次重复计算,大大地减少了程序代码。从代码的角度上来看就是函数调用自身,我们称之为递归。
2. 举例说明递归算法
我们现在用一个简单的例子进行说明:假设我们需要写一个函数去求数字n的阶乘。当输入5时,输出5!=120,当输入6时,输出6!=720。如果我们编写了一个函数 F(n) 用来求解输入参数 n 的阶乘值,很明显我们可以发现这样一个递归关系:F(n) = n * F(n - 1),那么我们求解 F(n) 的代码可以这样写:
递归求 5 的阶乘 Python 实现
def F(n):
if n == 1:
return 1
return n \* F(n - 1)
前两行的语句是递归终止条件,这个是必须要有的,而且必须是递归要能到达的。最后一个 n * F(n - 1) 正是递归调用自身,且每次递归的参数都会减少直到最后的终止条件结束。我们用示例图来演示下 F(5) 执行的递归过程,这样方便我们理解递归调用。
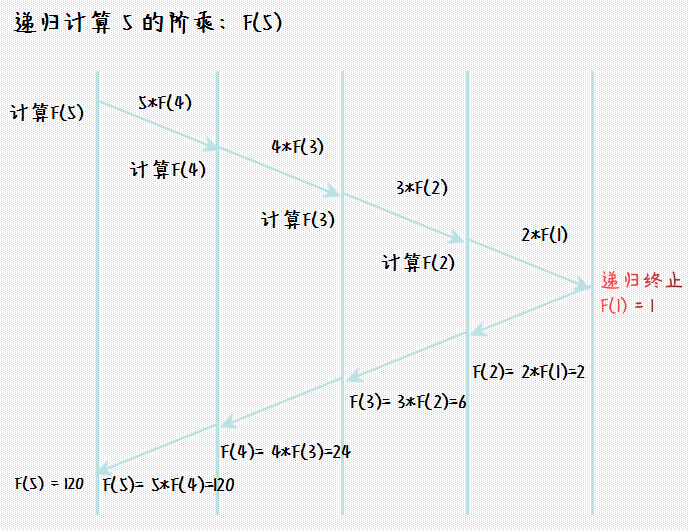
计算F(5)的递归调用 递归算法动态示意图:

从上面的示意图可以看到,递归的思想就是在不停调用本身往下执行,直到终止条件达到然后再回推结果。递归带来的好处非常明显,就是减少代码,让代码看起来简洁明了。假如我们要使用非递归算法来求解 n 的阶乘,代码如下:
def F\_no\_recursive(n):
s = 1
for i in range(1, n + 1):
s = s \* i
return s
可以看到,递归代码相比不使用递归的代码少了 for 循环,并且递归的代码看起来会比较简洁和清楚,这在二叉树的问题中会体现的非常明显。
3. 函数调用过程
在所有的编程语言中,函数的调用都是这样的过程:
- 将当前调用函数的下一个指令地址压入堆栈,并保存现场环境;
- 调到调用函数地址去执行;
- 调用函数执行完成后,调用
ret指令弹出下一步执行的地址,返回到原来的函数中接着执行下一条语句。
示意图如下:
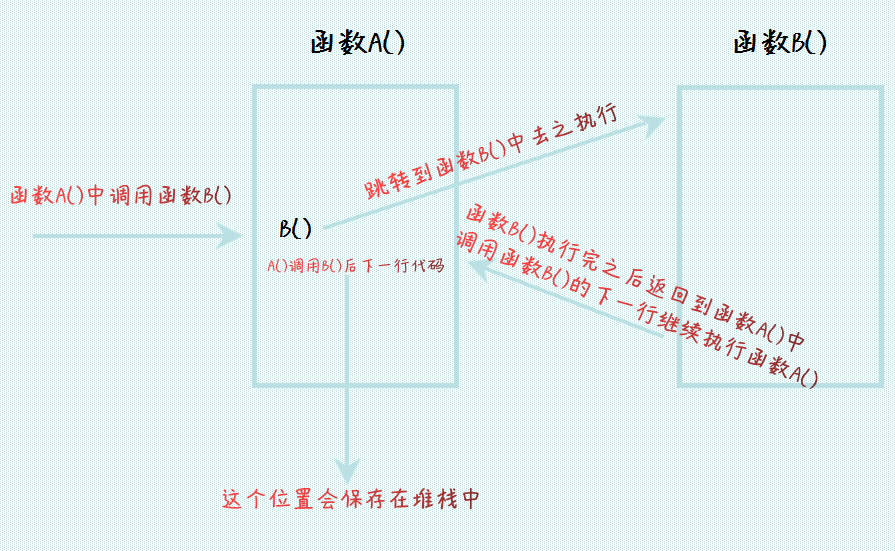
函数调用过程 自己调用也是一样的过程,并不会说自己调用自己递归就会在函数内部执行,同样是在另一个地址有一份相同的函数代码拷贝,也就是将上图中的函数 B() 换成函数 A(),这幅图同样正确。递归调用的示意图如下:
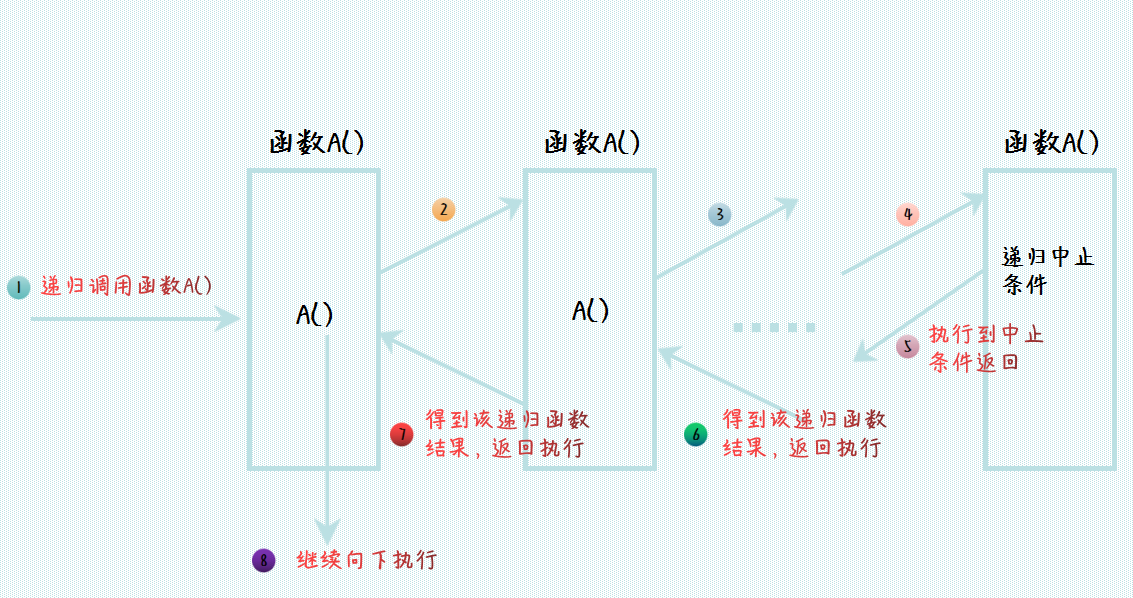
递归调用示意图
4. 递归算法的缺点
前面说到了递归问题的优点,就是使用递归后整体代码简洁明了,阅读起来让人如沐春风。但是递归方法也会才能在较大问题:
- 递归太深,容易导致栈溢出异常。前面介绍过,函数调用是通过栈(stack)这种数据结构实现的,每当进入一个函数调用,栈就会加一层栈帧,每当函数返回,栈就会减一层栈帧。由于栈的大小不是无限的,所以,递归调用的次数过多,会导致栈溢出;
- 可能存在大量的冗余计算,算法的时间复杂度呈指数级增长,这个会在后面的递归实例中展示。
5. 解决递归问题的通用思路
对于一个递归问题,我们会有一套模板去实现这样一个递归算法:
- 递归终止条件:一定和必须要有;
- 递归公式:递归的核心,找不出递归公式的,也就无法使用递归算法来解决。这里实现递归算法的递部分;
- 返回预定结果:返回我们预先定好的结果参与递归算法的归部分;
基本上完成这样三个步骤,一个简易的递归算法也就算完成了,剩下的就是按照这三部实现代码了。我们不妨用前面的递归函数来看看这三步的具体位置:

递归三部曲 在下一节中,我们会在 LeetCode 上完成 3 道和递归相关的算法题,并使用这三个步骤去完成相关题解,也会让大家加深对这三步的理解。
6. 小结
本节在介绍了递归算法概念并对递归算法的优缺点进行了相关分析,紧接着用 leetcode 上的两道基础递归题目进行了练习和说明,帮助理解递归算法。
Tips:文中动图制作参考:https://visualgo.net/zh/sorting。