快速排序

今天我们来聊一聊无论是在笔试还是面试中常常考到的，也是最经典和最高效的快速排序算法。它的平均时间复杂度为 O(NlogN)O(NlogN)O(NlogN)，空间复杂度为 O(1)O(1)O(1)。

1. 快速排序算法原理

快速排序算法是基于这样的思想：从待排序的列表选择一个基准数，然后将列表中比该基准数大的放到该数的右边，比该基准数小的值放到该基准数的左边；接下来执行递归操作，对基准数左边的待排序列表执行前面同样的操作，直到左边的列表有序，对于基准数右边的待排序列表也执行前面同样的操作，直到右边的列表有序。此时，整个列表有序。即对于输入的数组 nums[left:right]：

分解：以 nums[p] 为基准将 nums[left: right] 划分为三部分: nums[left:p-1]，nums[p] 和 a[p+1:right]，使得 nums[left:p-1] 中任何一个元素小于等于 nums[p]，而 nums[p+1:right] 中任何一个元素大于等于 nums[p]；
递归求解：通过递归调用快速排序算法分别对 nums[left:p -1] 和 nums[p+1:right] 进行排序；
合并：由于对 nums[left:p-1] 和 nums[p+1:right] 的排序是就地进行的，所以在 nums[left:p-1] 和 nums[p+1:right] 都已排好序后，不需要执行任何计算，nums[left:right] 就已经排好序了；

下面是算法示意图：

图片描述

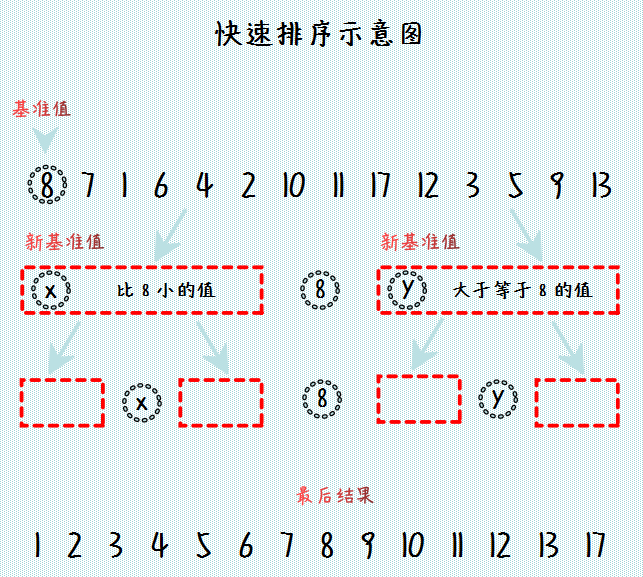
快速排序算法示意图

2. 快速排序空间复杂度优化

可以看到，上述快速排序算法的一个核心步骤是：**将列表中的比基准数小的全部移动到基准数的左边，其余数移动到基准数的右边，且整个算法的过程不能使用额外的空间。**这样的算法才比较高效，空间复杂度为 O(1)。那么怎么做到不使用额外空间达到这一目的呢？请看下面的示意图进行理解。

图片描述

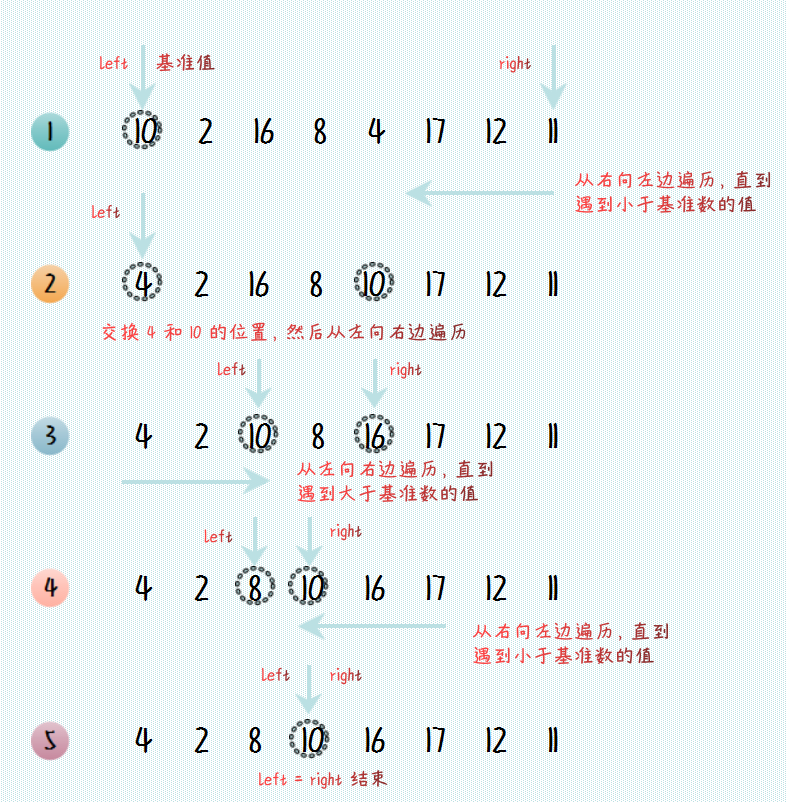
快速排序核心步骤可以看下快速排序动态图的演示：

图片描述

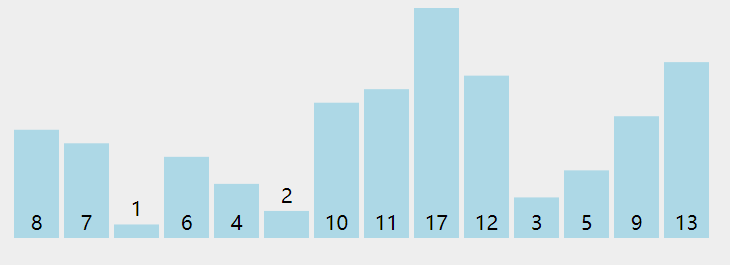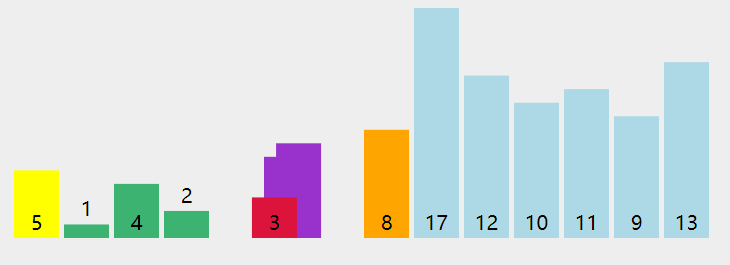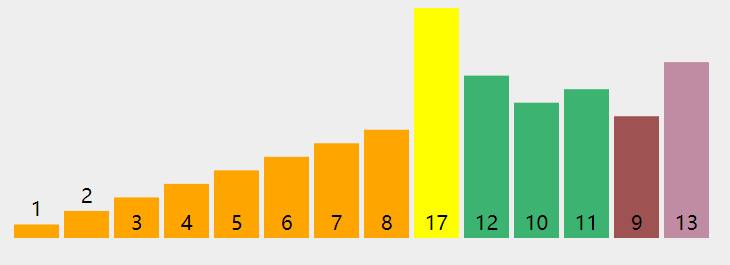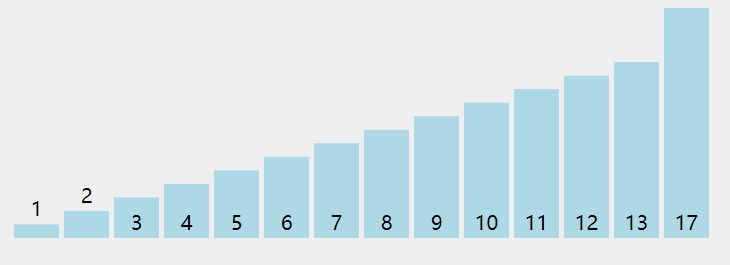
快速排序原理动态图演示接下来，我们就要使用 Python 实现上面的核心步骤以及最后的快排算法。

3. 快速排序算法的 Python 实现

首先我们实现上面的核心步骤，代码如下：

# 代码位置：sort\_algorithms.py

def get\_num\_position(nums, left, right):
    # 默认基准值为第一个
    base = nums[left]
    while left < right:
        # 从最右边向左直到找到小于基准值的数
        while left < right and nums[right] >= base:
            right -= 1
        # 将小于基准数的值放到右边，left原来位置放的是基准值(base)
        nums[left] = nums[right]
        # 然后从左边往右遍历，直到找到大于基准值的数
        while left < right and nums[left] <= base:
            left += 1
        # 然后将left位置上的值放到right位置上，right位置上的值原本为base值
        nums[right] = nums[left]
    # left=right的位置上就是基准值
    nums[left] = base
    return left

4. 实例测试快速排序代码

上面的函数中我们已经做了详细的注释，和前面第二张图描述的过程是一致的。接下来我们来对该方法进行测试：

PS C:\Users\spyinx\Desktop\学习教程\慕课网教程\算法慕课教程\code> python
Python 3.8.2 (tags/v3.8.2:7b3ab59, Feb 25 2020, 22:45:29) [MSC v.1916 32 bit (Intel)] on win32
Type "help", "copyright", "credits" or "license" for more information.
>>> from sort_algorithms import get_num_position
>>> nums = [10, 2, 16, 8, 4, 17, 12, 11]
>>> get_num_position(nums, 0, len(nums) - 1)        
3
>>> nums      
[4, 2, 8, 10, 16, 17, 12, 11]

可以看到，代码确实实现了我们想要的结果，将比 10 小的全部移动到了左边，比 10 大的全部移动到了右边。接下来就是实现快速排序算法。从第一张图中很明显可以看到快排算法是一个递归的过程，因此我们用递归完成快排算法，代码如下：

# 代码位置：sort\_algorithms.py

def quick\_sort(nums, start, end):
    """
 快速排序算法
 """
    if start >= end:
        return 
    pos = get_num_position(nums, start, end)
    # 左边递归下去，直到排好序
    quick_sort(nums, start, pos - 1)
    # 右边递归下去，直到排好序
    quick_sort(nums, pos + 1, end)

对于递归方法，后面会详细介绍到。这里一定要注意，使用递归过程一定要先写终止条件，不然函数无穷递归下去，就会导致堆栈溢出错误。接下来我们测试这个快排算法：

>>> from sort_algorithms import quick_sort
>>> nums = [8, 7, 9, 6, 11, 3, 12, 20, 9, 5, 1, 10]
>>> quick_sort(nums, 0, len(nums) - 1)
>>> nums
[1, 3, 5, 6, 7, 8, 9, 9, 10, 11, 12, 20] 

可以看到上面的代码实现了我们想要的排序效果。接下来我们分析下快排算法，它被人们研究的最多，提出了许多改进和优化的方案，我们简单聊一下快排算法的优化方案。

5. 优化快速排序算法

对于优化快速排序，在这里我们只考虑最简单的一种优化思路，就是基准数的选择。前面的快排算法中，我们都是选择列表的第一个元素作为基准数，这在列表随机的情况下是没有什么问题的，但对本身有序的列表进行排序时，时间复杂度就会退化到 O(n2)O(n^2)O(n2)。我们来进行相关测试：

# 冒泡排序算法
import datetime
import random
from sort_algorithms import get_num_position, quick_sort

# python默认递归次数有限制，如果不进行设置，会导致超出递归最大次数
import sys   
sys.setrecursionlimit(1000000)

if __name__ == '\_\_main\_\_':
    # 对于设置10000，本人电脑会出现栈溢出错误
    # nums = [random.randint(10, 10000) for i in range(6000)] 
    nums = [i for i in range(6000)] 
    start = datetime.datetime.now()
    quick_sort(nums, 0, len(nums) - 1)
    end = datetime.datetime.now()
    print('Running time: %s Seconds' % (end-start))

第一个注释的语言是对 nums 列表随机生成，而第二个直接情况是直接生成有序的列表。我们分别看执行结果：

# 随机列表快排
PS C:\Users\spyinx\Desktop\学习教程\慕课网教程\算法慕课教程\code> & "D:/Program Files (x86)/python3/python.exe" c:/Users/spyinx/Desktop/学习教程/慕课网教程/算法慕课教程/code/test_algorithms.py
Running time: 0:00:00.027907 Seconds

# 有序列表快排
PS C:\Users\spyinx\Desktop\学习教程\慕课网教程\算法慕课教程\code> & "D:/Program Files (x86)/python3/python.exe" c:/Users/spyinx/Desktop/学习教程/慕课网教程/算法慕课教程/code/test_algorithms.py
Running time: 0:00:02.159677 Seconds

可以看到明显的差别，差不多差了 80 倍，这确实是纯快排算法存在的一个问题。如果我们往这个有序列表中插入少量随机数，打破有序的情况，会看到性能会有较大提升。这个问题的根源在于基准数目的选择，对于有序的列表排序时每次都是选择的最小或者最大的值，这就是最坏的情况。一个显而易见的改进策略就是随机选择列表中的值作为基准数，另一种是从头 (left)、中 ([left + right] // 2) 和尾 (right) 这三个元素中取中间值作为基准数。我们分别进行测试：

import random
def get\_base(nums, left, right):
    index = random.randint(left, right)
    if index != left:
        nums[left], nums[index] = nums[index], nums[left]
    return nums[left]


def get\_base\_middle(nums, left, right):
    if left == right:
        return nums[left]
    mid = (left + right) >> 1

    if nums[mid] > nums[right]:
        nums[mid], nums[right] = nums[right], nums[mid]

    if nums[left] > nums[right]:
        # nums[left]最大，nums[right]中间，所以交换
        nums[left], nums[right] = nums[left], nums[mid]

    if nums[mid] > nums[left]:
        # 说明nums[left]最小, nums[mid]为中间值
        nums[left], nums[mid] = nums[mid], nums[left]

    return nums[left]


def get\_num\_position(nums, left, right):
    # base = nums[left]
    # 随机基准数
    base = get_base(nums, left, right)
    # base = get\_base\_middle(nums, left, right)
    while left < right:
        # 和前面相同，以下两个while语句用于将基准数放到对应位置，使得基准数左边的元素都小于它，右边的数都大于它
        while left < right and nums[right] >= base:
            right -= 1
        nums[left] = nums[right]
        while left < right and nums[left] <= base:
            left += 1
        nums[right] = nums[left]
    # 基准数的位置，并返回该位置值
    nums[left] = base
    return left

改进后的测试结果如下：

# 有序列表-随机基准值
PS C:\Users\spyinx\Desktop\学习教程\慕课网教程\算法慕课教程\code> & "D:/Program Files (x86)/python3/python.exe" c:/Users/spyinx/Desktop/学习教程/慕课网教程/算法慕课教程/code/test_algorithms.py
Running time: 0:00:00.021890 Seconds

# 随机列表-随机基准值
PS C:\Users\spyinx\Desktop\学习教程\慕课网教程\算法慕课教程\code> & "D:/Program Files (x86)/python3/python.exe" c:/Users/spyinx/Desktop/学习教程/慕课网教程/算法慕课教程/code/test_algorithms.py
Running time: 0:00:00.026948 Seconds

# 有序列表-中位数基准值
PS C:\Users\spyinx\Desktop\学习教程\慕课网教程\算法慕课教程\code> & "D:/Program Files (x86)/python3/python.exe" c:/Users/spyinx/Desktop/学习教程/慕课网教程/算法慕课教程/code/test_algorithms.py
Running time: 0:00:00.012944 Seconds

# 随机列表-中位数基准值 
PS C:\Users\spyinx\Desktop\学习教程\慕课网教程\算法慕课教程\code> & "D:/Program Files (x86)/python3/python.exe" c:/Users/spyinx/Desktop/学习教程/慕课网教程/算法慕课教程/code/test_algorithms.py
Running time: 0:00:00.020933 Seconds

可以看到使用中位数基准值在有序列表情况下排序速度更快。最后还有一个简单的常用优化方案，就是当序列长度达到一定大小时，使用插入排序。

# 改造前面的插入排序算法
def insert\_sort(nums, start, end):
    """
 插入排序
 """
    if not nums:
        return False
    for i in range(start + 1, end + 1):
        t = nums[i]
        for j in range(i - 1, start - 1, -1):
            k = j
            if nums[j] <= t:
                k = k + 1
                break
            nums[j + 1] = nums[j]
        nums[k] = t
    return True 

# ...

def quick\_sort(nums, start, end):
    """
 快速排序算法
 """
    if (end - start + 1 < 10):
        # 在排序的数组小到一定程度时，使用插入排序
        insert_sort(nums, start, end)
        return
    # 找到基准数位置，同时调整好数组，使得基准数的左边小于它，基准数的右边都是大于它
    pos = get_num_position(nums, start, end)
    # 递归使用快排，对左边使用快排算法
    quick_sort(nums, start, pos - 1)
    # 对右边元素使用快排算法
    quick_sort(nums, pos + 1, end)

下面是使用【随机基准+插入排序优化】的测试结果如下：

# 有序列表-[随机基准+使用插入排序优化]
PS C:\Users\spyinx\Desktop\学习教程\慕课网教程\算法慕课教程\code> & "D:/Program Files (x86)/python3/python.exe" c:/Users/spyinx/Desktop/学习教程/慕课网教程/算法慕课教程/code/test_algorithms.py
Running time: 0:00:00.010962 Seconds

# 无序列表-[随机基准+使用插入排序优化]
PS C:\Users\spyinx\Desktop\学习教程\慕课网教程\算法慕课教程\code> & "D:/Program Files (x86)/python3/python.exe" c:/Users/spyinx/Desktop/学习教程/慕课网教程/算法慕课教程/code/test_algorithms.py
Running time: 0:00:00.018935 Seconds

可以看到这些小技巧在真正大规模数据排序时会有非常明显的效果。更多的优化方法以及测试，读者可以自行去实验和测试，这里就不再继续讲解了。

6. 小结

本小节我们介绍了快速排序算法以及相关的优化策略，并完成了简单的实验测试，方便大家理解改进的效果。至此，排序算法介绍到此就要结束了。当然高效的排序算法并不止快排算法，海域堆排序、归并排序、桶排序以及基数排序等等，这些读者可以自行学习并实现相关代码，打好算法基础。

Tips：文中动图制作参考：https://visualgo.net/zh/sorting。

快速排序

1. 快速排序算法原理​

2. 快速排序空间复杂度优化​

3. 快速排序算法的 Python 实现​

4. 实例测试快速排序代码​

5. 优化快速排序算法​

6. 小结​

1. 快速排序算法原理

2. 快速排序空间复杂度优化

3. 快速排序算法的 Python 实现

4. 实例测试快速排序代码

5. 优化快速排序算法

6. 小结