分治算法实战

今天我们通过 3 道 leetcode 算法题来实战分治法。3道题的难度分别为简单、中等和中等，各有特色。让我们一起来领略分治的魅力吧。

1. 连续数列

首先看题目，这是 leetcode 中的面试题部分，题目内容如下：

给定一个整数数组，找出总和最大的连续数列，并返回总和。

示例：

输入： [-2,1,-3,4,-1,2,1,-5,4]

输出： 6

解释： 连续子数组 [4,-1,2,1] 的和最大，为 6。

进阶：如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的分治法求解。

这个很明显是一道动态规划问题，而且使用动态规划方法的时间复杂度为 O(n)O(n)O(n)，空间复杂度可以优化为 O(1)O(1)O(1)。题目描述中已经说明了可以使用分治法去求解该问题。那我们就要思考，如何分解问题，如何合并子问题的解。首先定义解决该问题的方法：

def divide(nums, left, right):
    """
 返回nums[left:right+1]总和最大的连续数列
 """
    pass

分解终止条件

当数组为空时，我们就可以停止分解了，转而合并结果：

if left == right:
    return nums[left]

分解问题

每次将序列对半分割即可，然后使用递归得到子问题的解：

# 中间一分为二
mid = (left + right) // 2

# 递归法：得到左边最大子序列和，不包含右边序列
leftSum = divide(nums, left, mid)
# 递归得到右边最大子序列和，不包含mid及其左边序列
rightSum = divide(nums, mid + 1, right)

合并子问题的解

这是最关键的一步，上面把序列规模进行对半分割后，我们需要通过左边序列的解和右边序列的解一起来得出最终的完整序列的解。

假设我们定义方法： divide(nums, left, right) 为序列 nums[left:right+1] 中最大连续子列的和；

进行规模分割，有 mid=(left + right) // 2，那么原来的列表被划分为两个子列表：nums[left, mid+1] 和 nums[mid+1, right]。

此时 divide(nums, left, mid) 结果表示列表 nums[left:mid+1] 中的最大子序列和，记为 leftSum，而 divide(nums, mid+1, right) 的结果表示的是 nums[mid+1:right] 中的最大子序列和，记为 rightSum。

那么我们仅拿着左右着两边最大子序列和的最大值，即 max(leftSum, rightSum) 来作为原问题的解，是否可行？

显然是不行的，因为如果原问题的最大连续子列并不单独在左边和右边，而可能同时包含左子列和右子列的元素：

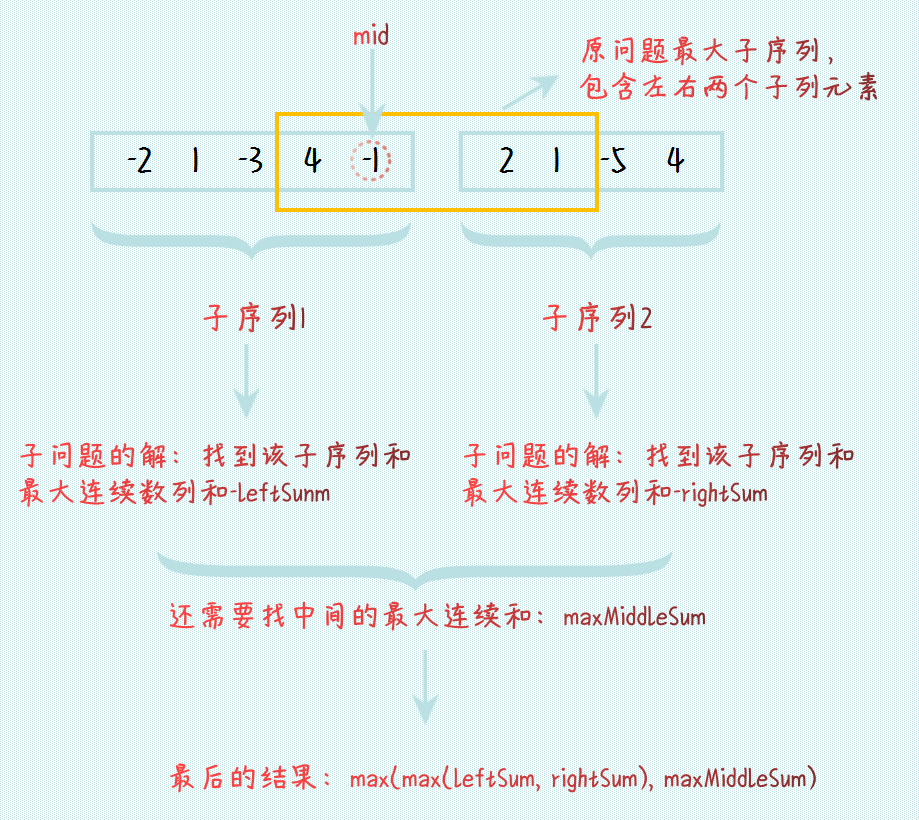
分治解法思路 此时，我们需要考虑如何从左右子序列中找到包含左右子序列元素的最大连续子序列和。

因为序列连续，所有会比较简单，我们直接从 mid 开始分别往左边移动，计算包含每个元素的连续和 (该元素到 mid 位置的元素全部要包括)，找到最大值，得到 leftMidSum。

右边的子序列做同样的操作，得到 rightMidSum。最后这两个值的和就是同时包含左右子序列元素的最大连续数列的和：leftMidSum + rightMidSum。

这个时候我们在拿这三个的值进行比较，找到最大值，此时得到的结果才是原问题的解：max(max(leftSum, rightSum), leftMidSum + rightMidSum)。

寻找包含左右子列元素的最大连续数列和 上述实现查找包含左右连续子序列最大和的方法如下：

# 从找出包含mid的左边连续序列的最大值
leftVal = 0 
leftMidSum = nums[mid] - 1
for i in range(mid, left - 1, -1):
    leftVal += nums[i]
    leftMidSum = max(leftVal, leftMidSum)
    
# 找出右边序列中最大值
rightVal = 0 
rightMidSum = nums[mid + 1] - 1
for i in range(mid + 1, right + 1):
    rightVal += nums[i]
    rightMidSum = max(rightVal, rightMidSum)

最后原问题的解为三个值中的最大值，即：

max(max(leftSum, rightSum), leftMidSum + rightMidSum)

通过上述分析，我们最终得到如下 Python 代码：

def maxSubArray(nums):
    """
 分治法
 """   
    def divide(nums, left, right):
        if left == right:
            return nums[left]
        # 中间一分为二
        mid = (left + right) // 2
        
        # 递归法：得到左边最大子序列和，不包含右边序列
        leftSum = divide(nums, left, mid)
        # 递归得到右边最大子序列和，不包含mid及其左边序列
        rightSum = divide(nums, mid + 1, right)

        # 从找出包含mid的左边连续序列的最大值
        leftVal = 0 
        leftMidSum = nums[mid] - 1
        for i in range(mid, left - 1, -1):
            leftVal += nums[i]
            leftMidSum = max(leftVal, leftMidSum)

        # 找出右边序列中最大值
        rightVal = 0 
        rightMidSum = nums[mid + 1] - 1
        for i in range(mid + 1, right + 1):
            rightVal += nums[i]
            rightMidSum = max(rightVal, rightMidSum)
        # 此时leftMidSum + rightMidSum便是中间包含mid的连续子序列的最大值
        return max(max(leftSum, rightSum), leftMidSum + rightMidSum)

    return divide(nums, 0, len(nums) - 1)          

这个执行的时间复杂度为 O(nlogn)O(nlogn)O(nlogn)，提交代码耗时在所有 Python3 提交中垫底，但是这个解题的思路却是很重要的，锻炼我们分治求解能力。

2. 最小 K 个数

来看一道常见的面试题，题目描述如下：

设计一个算法，找出数组中最小的k个数。以任意顺序返回这k个数均可。

示例：

输入： arr = [1,3,5,7,2,4,6,8], k = 4
输出： [1,2,3,4]

Tips：

• 0 <= len(arr) <= 100000；
• 0 <= k <= min(100000, len(arr))；

其实不用分治法，直接考虑快排之后选择前 k 个数即能通过题解。但是本题我们要换一种思路，使用分治法来解决该题。首先定义解决原问题的方法：

def divide(arr, left, right, k):
    """
 找出arr[left:right+1]中的最小k个数并返回 
 """
    pass

终止条件

很明显，我们要找数组中最小的 k 个数，如果数组长度为空或者长度小于 k，我们可以直接返回该数组：

# 注意 left 和 right 用于限定数组

# 终止条件
if not k:
    return []
# 终止条件
if (right - left + 1) <= k:
    return arr[left: right + 1]

分解列表

和之前一样，都是对半分，mid = (left + right) // 2，那么数组会被划分为如下两个部分：

arr[left:mid + 1] # 左半部分
arr[mid + 1:right] # 右半部分

对于的子问题的解为：

# 得到左子列的最小k个数
arr_left_k = divide(arr, left, mid, k)
# 得到右子列的最小k个数
arr_right_k = divide(arr, mid + 1, right, k)

合并子结果，得到原问题的解

首先定义方法：divide(nums, left, right, k)，该方法会找出列表 nums[left:right + 1] 中前最小的 k 个数。

我们用分治法后，将列表分成两个子列：nums[left:mid + 1] 和 nums[mid + 1:right + 1]。这样方法 divide(nums, left, mid, k) 返回的结果是左子列中前 k 个最小值，方法 divide(nums, mid + 1, right, k) 返回的结果是右边子列中前 k 个最小值。

此时我们知道，整个数组的前 k 个最小值必定在这 2k 个元素中。那么接下来的问题就是从这两 k 个值中找出最小的 k 个数即可，简单点的方式就是快排后取前 k 个。当问题规模 n 远大于 k 时，我们会发现排序所耗时间 O(klogk)O(klogk)O(klogk) 非常小，这样也决定了该分治算法的高效性。

# 组成2k个数的列表
arr_k = []
for i in range(len(arr_left_k)):
    arr_k.append(arr_left_k[i])
    arr_k.extend(arr_right_k)
# 使用快排方法，取前k个数，即为结果，直接返回
arr_k.sort()

最后返回我们想要的前 k 个元素即可：

return arr_k[:k]

综合上述几点，我们得到了如下完整的 Python 实现：

def smallestK(arr, k):
    def divide(arr, left, right, k):
        # 终止条件
        if not k:
            return []
        # 终止条件
        if (right - left + 1) <= k:
            return arr[left: right + 1]
        # 分治法
        mid = (left + right) // 2
        # 得到左子列的最小k个数
        arr_left_k = divide(arr, left, mid, k)
        # 得到右子列的最小k个数
        arr_right_k = divide(arr, mid + 1, right, k)

        # 组成2k个数的列表
        arr_k = []
        for i in range(len(arr_left_k)):
            arr_k.append(arr_left_k[i])
        arr_k.extend(arr_right_k)
        # 使用快排方法，取前k个数，即为结果，直接返回
        arr_k.sort()
        return arr_k[:k]

    return divide(arr, 0, len(arr) - 1, k)

最后提交测试，处于中上游水平。这道题目比较经典的做法是使用堆排序的方法，得到的最小 k 个数，大家可以课后使用堆排序的方法完成。

3. 漂亮数组

这一题是 leetcode 上算法部分的第932题：漂亮数组。该题的描述如下：

对于某些固定的 N，如果数组 A 是整数 1, 2, …, N 组成的排列，使得：对于每个 i < j，都不存在 k 满足 i < k < j 使得 A[k] * 2 = A[i] + A[j]。那么数组 A 是漂亮数组。给定 N，返回任意漂亮数组 A（保证存在一个）。

示例 1：

输入：4
输出：[2,1,4,3]

示例 2：

输入：5
输出：[3,1,2,5,4]

这道题官方给出了一个非常精妙的分治思路，接下来我们一起来领略下分治的魅力。和前面所有的解答一样，先对数组进行分解，然后分别通过子问题的解来得到原问题的解。

首先是原问题的解是：得到长度为 N 的漂亮数组，该数组的元素是 1~N 的一个全排列。我们定义这样一个方法，实现这个问题的解：f(N)，接下来对 N 进行对半分解，得到 f((N + 1) // 2) 和 f(N // 2)，它们分别返回长度为 ( N +１) // 2 和 N // 2 的漂亮数组，那么如何将这两个漂亮数组组成长度为 N 的漂亮数组呢？

注意： f((N + 1) // 2) 得到的漂亮数组是 1~((N + 1) // 2) 的一个全排列， 而 f(N // 2) 得到的漂亮数组是 1~(N // 2) 的全排列，而最终 f(N) 得到的漂亮数组为 1~N 的一个全排列。

官方指出了该漂亮数组的一个性质：如果某个数组 [a1, a2, … ,an] 是漂亮的，那么数组 [ka<sub>1</sub>+b, ka<sub>2</sub>+b, ... ,ka<sub>n</sub>+b] 也是漂亮的。假设我们将 f((N + 1) // 2) 和 f(N // 2) 得到的结果组合到一起：

x=[a1,a2,⋯,aN+12,b1,b2,⋯,bN2] x = [a_1,a_2,\cdots,a_\frac{N+1}{2},b_1,b_2,\cdots,b_\frac{N}{2}] x=[a1​,a2​,⋯,a2N+1​​,b1​,b2​,⋯,b2N​​]

我们注意到，前半部分为漂亮数组，后半部分也是漂亮数组，也就是满足漂亮的特点。现在还需要两个条件：

• 将数组变成 1~N 的全排列；
• 保证从 a 数组中取一个 a[i]，从 b 数组中取一个 b[j]，然后不存在 i<k<(N+1)//2 + j，使得 x[k] * 2 = a[i] + b[j]。

如何能实现上述两个条件呢？看公式：A[k] * 2 = A[i] + A[j]， 发现 A[k] * 2 为偶数，那么只要 A[i] 和 A[j] 分别为奇数和偶数，那么这个式子就不会成立。对于如何满足上面的条件二，我们只需要通过将 a 的漂亮数组进行奇数映射即可，同样对于 b 的漂亮数组进行偶数映射即可：

x1 = [2 \* x - 1 for x in a]   # 得到奇数
x2 = [2 \* x for x in b]       # 得到奇数

主要到这样映射后，得到的 x1 和 x2 仍旧是漂亮数组，且 x1 为奇数数组，x2为偶数数组。从 x1 和 x2 中各自选一个元素 ，永远不会由这两个元素的中间元素 m 满足：m * 2 = x1 + x2 （因为 x1 为奇数，x2 为偶数，而 m * 2 为偶数）。

更巧的是，这样映射之后，x1 和 x2 中的元素正好是 1~N 的一个全排列，这样就通过两个子问题的解最终得到了原问题 f(N) 的解。是不是非常巧妙？下面官方题解给出的关于上述分治算法的精妙解答，用的正是上面的分治思路：

def beautifulArray(N):
    memo = {1: [1]}
    def f(N):
        if N not in memo:
            # 得到长度为 (N + 1) // 2 的漂亮数组
            odds = f((N + 1) // 2)
            # 得到长度为 N // 2 的漂亮数组
            evens = f(N // 2)
            # 组合成长度为 N 的漂亮数组，基于的上面讨论的规则
            memo[N] = [2 \* x - 1 for x in odds] + [2 \* x for x in evens]
        return memo[N]
    return f(N)

总的来说，分治法有很多应用场景，且经常使用会结果递归来实现。但并不是所有的题目都适合分治法，我们要看通过分割问题规模而得到的子问题的解，究竟能不能合并得到原问题的解，这才分治算法的核心。

4. 小结

本小节使用了 3 道 leetcode 编程题进行了分治算法的实战练习，通过这些题目可以加深我们对分治算法的理解及应用。在 leetcode 以及其他 OJ 平台上还有很多这样有意思的题目，大家要勤于练习。Python 基础算法教程的内容就到这里结束了，感谢大家的阅读与陪伴，咱们青山不改，江湖再会。