动态规划算法介绍

今天我们来介绍基础算法中非常重要而且又略微烧脑的算法：动态规划 (Dynamic Programming, 简称DP) 算法。

1. 动态规划算法介绍

动态规划算法的基本思想与分治法类似，也是将待求解的问题分解为若干个子问题（阶段），按顺序求解子阶段，前一子问题的解，为后一子问题的求解提供了有用的信息。

在求解任一子问题时，列出各种可能的局部解，通过决策保留那些有可能达到最优的局部解，丢弃其他局部解。依次解决各子问题，最后一个子问题就是初始问题的解。

2. 动态规划算法过程

动态规划过程是：每次决策依赖于当前状态，又随即引起状态的转移。一个决策序列就是在变化的状态中产生出来的，因此，这种多阶段最优化决策解决问题的过程就称为动态规划。

动态规划的本质，是对问题状态的定义和状态转移方程的定义。动态规划是通过拆分问题，定义问题状态和状态之间的关系，使得问题能够以递推（或者说分治）的方式去解决。因此在一个典型的动态规划问题上，我们需要能定义问题状态以及写出状态转移方程，这样对于该问题的解答就会一目了然。我们用一个经典的最长上升子序列问题对此进行说明。

3. 举例说明动态规划算法

最长上升子序列 (LIS) 问题如下：

给定一个无序的整数数组，找到其中最长上升子序列的长度。

示例：

输入：[10, 9, 2, 5, 3, 7, 101, 18]
输出：4 
解释：最长的上升子序列是 [2,3,7,101]，它的长度是 4。

来看看具体的动图演示：

动态规划算法动图演示 对于这个非常典型的动态规划问题，我们首先考虑如何定义问题的状态。一种简单的状态定义如下：

f(x)f(x)f(x) 为以 axa_xax​ 结尾的 LIS 长度,那么 LIS 的答案就是max{f(x)}max{f(x)}max{f(x)}

4. 推导动态规划状态转移方程

有了这样一个状态定义，我们来推导状态转移方程。来看如下示意图：

求f(6)的推导 从上面的图中，我们可以很明显得到该问题的状态转义方程，如下：

F(x)=maxp<x,ap<ax{F(p)+1} F(x) = max_{p<x,a_p<a_x}{F(p) + 1} F(x)=maxp<x,ap​<ax​​{F(p)+1}

于是有了这个状态方程我们就能很快写出相关的代码：

def lengthOfLIS(self, nums):
    if not nums:
        return 0

    n = 1
    F = [1]
    for i in range(1, len(nums)):
        max_num = 1
        for j in range(i - 1, -1, -1):
            if nums[i] > nums[j] and max_num < (F[j] + 1):
                max_num = F[j] + 1
                F.append(max_num)
        if F[-1] > n:
            n = F[-1]
    return n

这里的平均时间复杂度很明显为 O(n2)O(n^2)O(n2)。此外，对于该问题，我们还可以以另外一种角度考虑该问题，并定义一种二维状态：

给定一个数列，长度为 N，设 Fi,kF_{i,k}Fi,k​ 为：在前i项中的，长度为k的最长递增子序列中，最后一位的最小值为：1≤k≤N1 \leq{k}\leq{N}1≤k≤N

注意：若在前 i 项中，不存在长度为 k 的最长递增子序列，则 Fi,kF_{i,k}Fi,k​ 为正无穷.求最大的 x，使得 FN,xF_{N,x}FN,x​ 不为正无穷。

此时对应的状态转移方程如下：Ai>Fi−1,k−1A_i>F_{i-1,k-1}Ai​>Fi−1,k−1​，则 Fi,k=min(Ai,Fi−1,k)F_{i,k}=min(A_i,F_{i-1,k})Fi,k​=min(Ai​,Fi−1,k​)，否则Fi,k=Fi−1,kF_{i,k}=F_{i-1,k}Fi,k​=Fi−1,k​。大家可以自行思考下这个状态转移方程，动笔画一画。

5. 动态规划的深入理解

文献1中的第一个回答给出了动态规划的一些基本性质以及如何判断一个问题是否能使用 DP 解决。首先是基础概念：

• 无后效性：严格定义就是如果给定某一阶段的状态，则在这一阶段以后过程的发展不受这阶段以前各段状态的影响。也就是说未来与过去无关，这就是无后效性。
• 最优子结构：大问题的最优解可以由小问题的最优解推出，这个性质叫做最优子结构性质。

有了这两个概念之后，判断一个问题能否使用 DP 解决，就看该问题能否满足如下条件：大问题能拆成几个小问题，且满足无后效性、最优子结构性质。

我们以 leetcode 上的第 64 题最小路径和为例进行说明：

给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

注意：每次只能向下或者向右移动一步。

示例：

输入:
[
    [1,3,1],
    [1,5,1],
    [4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。

以上面的示例为例，我们首先看这个最小路径问题：

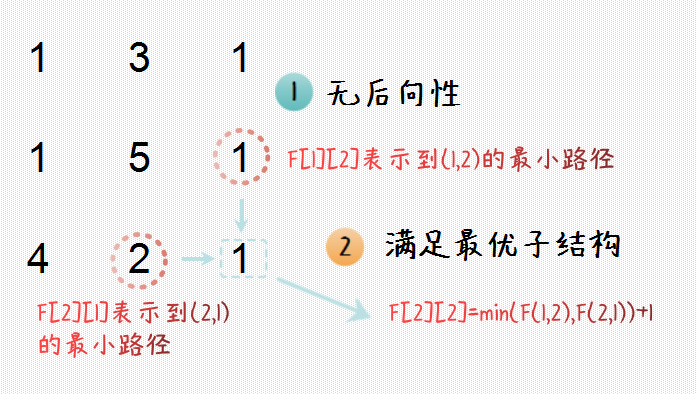
最小路径和问题DP特性分析 能理解该问题满足 DP 的两个特性，所以能用动态规划方法解决。我们定义状态：F[i][j]F[i][j]F[i][j]表示到(i,j)(i,j)(i,j)位置的最小路径和。

那么状态方转移方程也非常清楚，正如图中所示：

F[i][j]=min(F[i−1][j],F[i][j−1])+1 F[i][j]=min(F[i-1][j], F[i][j-1]) + 1 F[i][j]=min(F[i−1][j],F[i][j−1])+1

确定了核心步骤后，我们来看看问题的初始条件，类似于递归方法的终止条件。注意到每次只能向下或者向右移动一次，因此：

F[i][0]=F[i−1][0]+grid[i][0](i>0)∣grid[0][0](i=0)F[0][j]=F[0][j−1]+grid[0][j](j>0)∣grid[0][0](j=0) F[i][0] = F[i-1][0] + grid[i][0] (i > 0) \;|\; grid[0][0](i=0) F[0][j] = F[0][j-1] + grid[0][j] (j > 0) \;|\; grid[0][0](j=0) F[i][0]=F[i−1][0]+grid[i][0](i>0)∣grid[0][0](i=0)F[0][j]=F[0][j−1]+grid[0][j](j>0)∣grid[0][0](j=0)

于是得到最后的动态规划代码如下：

class Solution:
    def minPathSum(self, grid):
        if not grid:
            return 0

        F = []
        for i in range(len(grid)):
            F.append([0] \* len(grid[0]))

        # 边界条件，向下
        for i in range(len(grid)):
            if i == 0:
                F[i][0] = grid[i][0]
            else:
                F[i][0] = F[i - 1][0] + grid[i][0]
        # 边界条件，向右
        for j in range(len(grid[0])):
            if  j == 0:
                F[0][j] = grid[0][j]
            else:
                F[0][j] = F[0][j - 1] + grid[0][j] 
        
        # 动态转移方程
        for i in range(1, len(grid)):
            for j in range(1, len(grid[0])):
                F[i][j] = min(F[i - 1][j], F[i][j-1]) + grid[i][j]
        
        return F[-1][-1]

这题是一个二维 DP 的典型例题，非常有代表性。总结而言，对于 DP 问题，我们首先是分析该问题能否使用 DP 方法去解答。如果可以，就需要思考和定义问题的状态定义并找出状态转移方程。有了这些核心的步骤后，我们只需要再分析以下初始的边界条件，然后就可以动手开始实现该问题的 DP 代码了。

6. 小结

本节我们介绍了动态规划算法的相关概念以及涉及到的解题步骤，然后用两个经典的动态规划例子展示了一般动态规划问题的求解步骤。接下来我们会用 leetcode 上的习题进行动态规划实战，加深对其理解并熟练使用。

Tips：文中动图制作参考：https://visualgo.net/zh/sorting。