Numpy 的数组运算与广播
广播,是指 Numpy 在算术运算期间处理不同形状的数组的能力。
对数组的算术运算通常在相应的元素上进行。 如果两个阵列具有完全相同的形状,则这些操作被无缝执行,这一小节将通过数组的运算来展示广播的一些特征。
1. 常见的两种广播途径
1.1 相同大小的数组计算
如果两个数组的维度完全一致,那么运算过程是两个数组相应元素的逐个计算。
案例
定义两个完全一致的数组:
arr0 = np.array([[1, 2, 3], [4, 5, 6]])
arr1 = np.array([[5, 5, 5], [5, 5, 5]])
查看数组结构:
arr0
out:
array([[1, 2, 3],
[4, 5, 6]])
arr1
out:
array([[5, 5, 5],
[5, 5, 5]])
查看加法运算的结果:
arr0 + arr1
out:
array([[ 6, 7, 8],
[ 9, 10, 11]])
查看乘法运算的结果:
arr0 \* arr1
out:
array([[ 5, 10, 15],
[20, 25, 30]])
可以看到,如果数组的维度一致,那么广播则是对应位置的元素运算。
1.2 数组与标量的计算
广播机制的存在,允许运算发生在不同维度的数组之间,其中最典型的场景,是数组的标量的计算。所谓的标量,我们可以简单地将之视为是0维的数组。
案例
对于加法运算:
arr0 + 5
out:
array([[ 6, 7, 8],
[ 9, 10, 11]])
对于乘法运算
arr0 \* 5
out:
array([[ 5, 10, 15],
[20, 25, 30]])
对于幂运算:
arr0 \*\* 5
out:
array([[ 1, 32, 243],
[1024, 3125, 7776]], dtype=int32)
可以发现,对于上述效果,是数组每个元素分别与标量进行运算的结果。
直观地,我们发现,标量在这个二维数组上发生了传播(广播),标量沿着数组的两个维度扩散,直至扩散的结果和待计算的二维数组一致,最后进行计算。
2. 不同维度的数组运算
2.1 沿着一个维度进行广播
一种简单的场景是,两个数组有一定的相似性,即数组(n×m)和数组(1,m)。
案例
arr2 = np.array([[10, 20, 30]])
arr2
out:
array([[10, 20, 30]])
观察不同大小的数组的广播规则:
arr0 + arr2
out:
array([[11, 22, 33],
[14, 25, 36]])
arr0 \* arr2
out:
array([[ 10, 40, 90],
[ 40, 100, 180]])
观察发现,arr2沿着arr0的第二个维度扩展了,扩展到二者相匹配,再进行了对应的计算。
可以用一张简图来进行描述相加的过程:
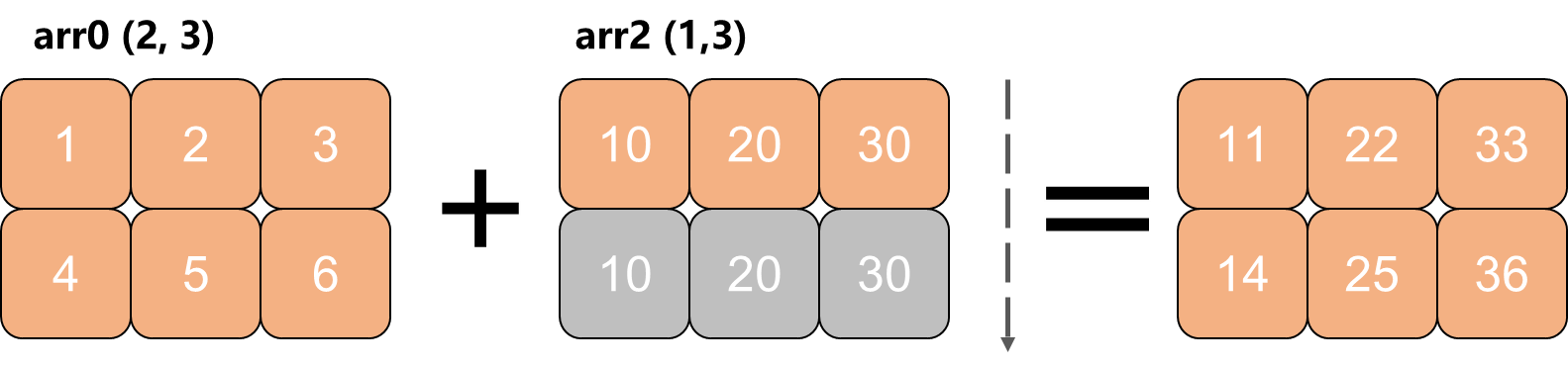
广播 1
2.2沿着两个维度同时广播
涉及到两个维度同时广播,则相对复杂一些。
案例
arr3 = np.array([[10], [20], [30]])
arr3
out:
array([[10],
[20],
[30]])
观察沿着2个方向同时广播的过程:
arr2 + arr3
out:
array([[20, 30, 40],
[30, 40, 50],
[40, 50, 60]])
上述广播的过程可以按照如下示意进行描述:
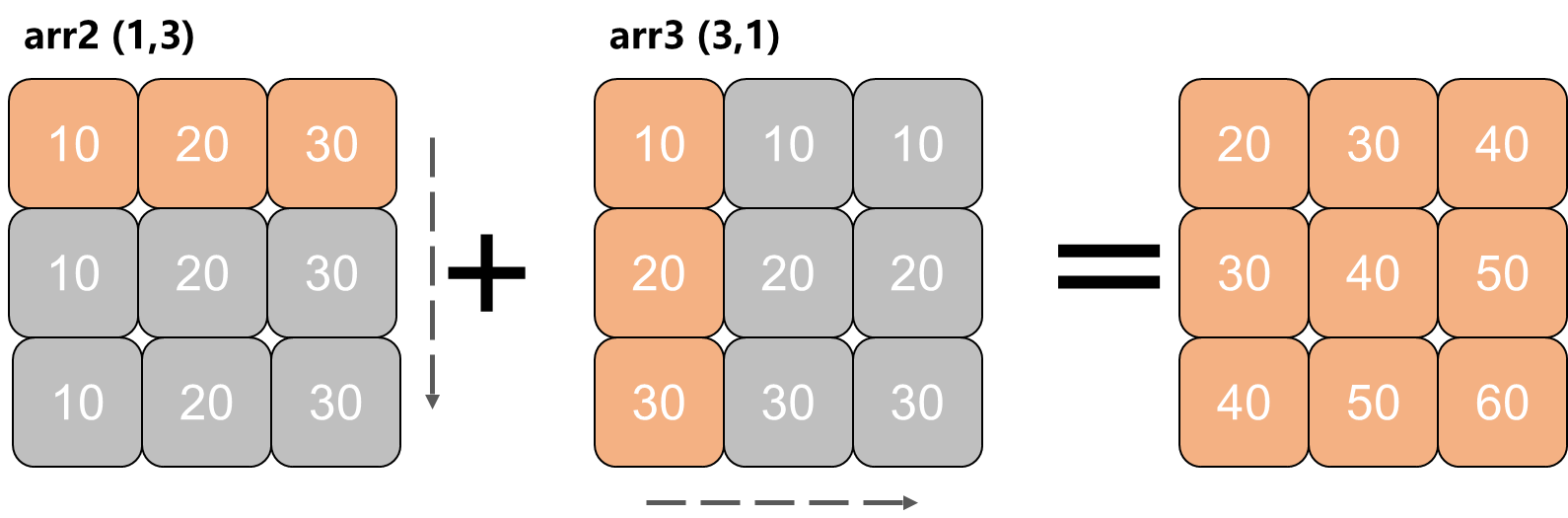
广播 2
2.3 广播的规则
所以根据上述案例,可以把广播规则简单总结如下:
- 让所有输入数组都向其中形状最长的数组看齐,形状中不足的部分都通过在前面加 1 补齐;
- 输出数组的形状是输入数组形状的各个维度上的最大值;
- 如果输入数组的某个维度和输出数组的对应维度的长度相同或者其长度为 1 时,这个数组能够用来计算,否则出错;
- 当输入数组的某个维度的长度为 1 时,沿着此维度运算时都用此维度上的第一组值。
3. 小结
本节以数组的运算为基础,介绍了数组在算术运算期间的广播规则。在实际使用中,广播的规则强大且灵活,当条件不满足时,则会抛出 ValueError: frames are not aligned 异常,需要注意。